
The Winner
Our winner is Jamie, a High School Student from Massachusetts, whose code surpasses in elegance my attempt at solving my own problem. Jamie gets the prize of £25 in Amazon gift vouchers. Honourable mention goes to Dan Dumitru who was the first to submit a solution.
Congratulations to Jamie, and thanks to all 10 of you who entered!
The Solution
The puzzle that Jamie and Dan solved was as follows;
Which Mathematicians have found themselves prime positions in the grid below?
So who were the coy Mathematicians, and how did they conceal themselves? Well, given the maths connection, “prime positions” must surely have something to do with prime numbers? So what happens if we count along the cells of the grid (wrapping over from the end of one row to the beginning of the following row) and note down the characters we find at indices which are prime-numbered?
Interesting! We get the string
tinyurl#teyuir#gqrtyh#hyirtq##
Teyuir? What theorem did he prove? must be Slovakian with a name like that. Now tinyurl – that rings a bell. Hey! I wonder what tinyurl.com/ teyuir looks like?
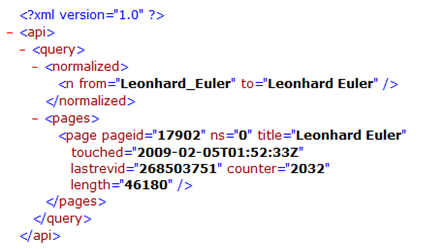
Huh! XML?
But wait: Leonhard Euler. There’s a name I recognise. Didn’t he dabble in mathematics, and prove a lemma or two?
And having reasoned thus, all that remains is to craft a handful of LINQ queries to winkle all three mathematicians out of the hiding places: Euler, Euclid and Cantor.
Here’s Jamie’s solution in its entirety. The code speaks for itself.
// Gets all the nonwhitespace characters
var rawChars = from ch in File.ReadAllText("HiddenMathematicians.txt")
where !char.IsWhiteSpace(ch)
select ch;
// Gets only the chars at prime indices (char[0] is at index 1)
var primeChars = from num in Enumerable.Range(2, rawChars.Count() - 1) // creates all indices from 1 to numRawChars
let divisors = Enumerable.Range(2, num - 2) // all possible divisors, 2 to num - 1
let isPrime = !divisors.Any(div => num % div == 0)
where isPrime
select rawChars.ElementAt(num - 1);
// All the words, including the beginning hint
var words = from str in primeChars.Aggregate(string.Empty, (str, ch) => str += ch).Split('#')
where !string.IsNullOrEmpty(str)
select str;
var names = from word in words.Skip(1)
let url = "http://" + words.First() + ".com/" + word
let xmlData = XDocument.Load(url)
let element = xmlData.XPathSelectElement("./api/query/pages/page")
let attribute = element.Attribute("title")
select attribute.Value;
foreach (var name in names)
Console.WriteLine(name);
Console.ReadLine();




10 comments:
=))
What's worse than losing a contest? Losing a contest where there are only two participants. :)
Now, I do admit it, Jamie's solution is clearly more elegant than mine. Using only query expressions permitted a way more compact solution than my seldom use of query operators.
I too would have picked his solution if I was the judge.
I still have to evilly add that my XML parsing was a bit nicer :p
So... Congratulations, Jamie!
I wonder what your's and Dan's solutions look like. In particular the XML parsing methods.
My XML parsing (with Linq-to-XML):
XElement root = XElement.Load(baseUrl + "/" + tag);
string hiddenMathematician = root.Descendants("page").SingleOrDefault().Attribute("title").Value;
(i hope the formatting won't be too screwed-up)
Oh...that is cleaner and not as unnecessarily verbose.
I should probably have added some sort of RangeFromTo instead of Enumerable.Range, which I kind of just put in mysterious numbers in.
My XML Parsing was the same as Dan's, though I'd forgotten that XElement.Load had the overload with a url as a parameter - so I wrote my own extension method using HttpRequest to fetch the XML!
@Jamie: I created a simple To() extension method, so that you can do 1.To(n) to get the sequence 1, 2, 3, ..., n:
http://blog.functionalfun.net/2008/04/project-euler-problem-4.html
Thanks, that could come in handy.
But I'm not sure about putting another method on int which may not make sense all the time. Would it be cleaner to have something like Range.FromTo(1, 5) or Range.From(1).To(5)? From(int) would return an RangeFromIntHolder which has a method .To(int). Or should I just use [int].To(int)?
Jamie, I've not had a problem with putting the method directly on int, but I take your point. I like your suggestion about Range.From(1).To(5). That reads very nicely.
Awesome work guys!
I would have been the third participant if not for the endless cocktail of laziness, school, homework and work from which I sip. I will definitely try to take part next time!
My first thoughts about the problem turned out to be the right ones to think, apparently, but I have to admit that I highly doubt I'd have come up with using the strange results as tinyurl links.
How did you guys figure that out? Is it because there is some standard length/composition of tinyurl links that you happened to know about, or are you guys just plain smarter than me? Hehe.
Oh, lol. I feel stupid. The first word says tinyurl.
Ah well, at least that means you guys don't possess some supernatural intelligence that I don't.
My XML parsing (with Linq-to-XML):
XElement root = XElement.Load(baseUrl + "/" + tag);
string hiddenMathematician = root.Descendants("page").SingleOrDefault().Attribute("title").Value;
(i hope the formatting won't be too screwed-up)
Post a Comment