Today we're going to talk about hailstones. No, not the sort that, last week, caused tens of millions of pounds of damage to 30,000 Volkswagen cars in an outside storage area in Germany. Rather the hailstones that are the subject of Project Euler Problem 14: hailstone numbers.
Hailstone numbers are just the kind of thing that fascinate mathematicians. You make them by picking any whole starting number, n, and then repeatedly applying one of the following two rules:
- if n is even, the next number is n/2
- if n is odd, the next number is 3n + 1
Try it; Start with 6. Then you get 6, 3, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, ... . Try it with another number. I bet you find yourself eventually writing 4, 2, 1, 4, 2, 1, ... all over again. If you don't, then, congratulations: you've just solved the Collatz problem, and won yourself at least a £1000 pound reward! You must also have picked a pretty big staring number. Using computers (obviously!) mathematicians have showed that if you kick off the sequence with any number smaller than about 2.7x1016 you'll eventually get down to the 4,2,1 repeating pattern.
You or I might be inclined to think, based on that evidence, that the sequence will always end in 4,2,1 for any starting number; but no quantity of successful tests would satisfy a pure-blooded mathematician: what if the next generation of computers tested even bigger numbers and found a sequence which didn't terminate like that? Hence the reward, which is being offered for a proof that for every whole number, the sequence generated by these rules eventually reaches 1; or, alternatively, for a demonstration of a number which begins a sequence that doesn't reach 1. This problem has taxed the minds of some of the brightest mathematicians for over 70 years.
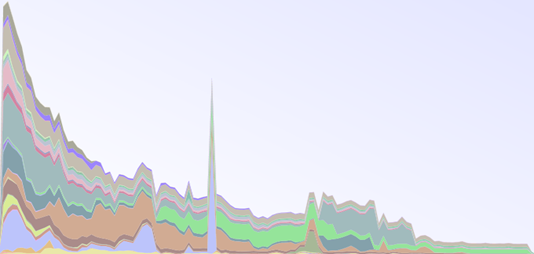
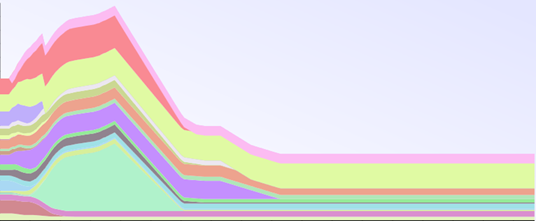
But why are they called Hailstone numbers? Have a look at this chart, where I've plotted a few sequences starting with different numbers: 
See how the sequences jump up and down? Apparently real hailstones do that when they're growing in the clouds: rising currents of air lift dust particles up into the clouds where they get smothered in ice; this makes them heavy, so they sink. Then the ice melts a little which makes them light enough to be pushed back up again- and so the little hailstones bounce up and down in the clouds getting fatter and fatter, until eventually they get so heavy that they fall to the ground, bouncing there until they come to a complete stop.
Now that you know the what and the why of Hailstone numbers, let's get to Euler's problem, which is to do with the length of sequences of hailstone numbers. We define the length of the sequence as being the number of terms up to the first occurrence of the number 1 (the example above starting with 6 has length 9, for example). Euler asks which starting number under 1 million produces the longest sequence?
A recursive solution
How to solve it? We could do it using an iterator or the Unfold method to generate the sequence, then counting the number of elements in it: but we're not actually interested in the numbers in the sequence, just the length of the sequence.
We can find the length of the sequence which starts at a particular number by finding the next term in the sequence, then adding one to the length of the sequence that starts at that term. In other words we can tackle this using a recursive function; and to make things interesting, we'll make it a recursive lambda function (this isn't gratuitous lambdaisation - you'll see why I've done it in a minute).
Func<long, long> findSequenceLength = null;
findSequenceLength = (long n) =>
{
if (n == 1) { return 1; }
var nextTerm = n.IsEven() ? n / 2 : 3* n + 1;
return findSequenceLength(nextTerm) + 1;
};
The trick to recursive lambda functions, as Eric Lippert pointed out, is to do what I've done in line 1 in the snippet above and assign null to the lambda before giving its actual definition; otherwise the compiler complains that the variable holding the lambda is being used before it is assigned.
Actually I'm misleading you a bit here, because we've not really created a recursive function at all. Thanks to the magic of closures, the lambda that we've assigned to findSequenceLength is really just calling the delegate stored in the variable findSequenceLength -that's why we need to be careful to assign that variable first (Wes Dyer explains more about this, and shows how to do real anonymous recursion in C#). But that very fact creates an opportunity for us: by changing the delegate that is stored in findSequenceLength we can subtly but usefully change the way findSequenceLength works.
Memoization
If you try out a couple of hailstone sequences, you'll soon discover that there are many that start off differently, but converge onto the same (bumpy) glide path down to the (4,2,1) ending. If you start with 24, for example, the third term in the sequence will be 6, and then will continue exactly the same as the sequence starting at 6. This means that once we have encountered one of these 'glide paths' and calculated its length, we really shouldn't need to do the same calculations all over again.
Memoization is a neat trick you can apply to give your lambdas a memory of what they've calculated before (thanks, again, to Wes Dyer for his post on memoization). Have a look at this code:
public static Func<T, TResult> Memoize<T, TResult>(this Func<T, TResult> function)
{
var cache = new Dictionary<T, TResult>();
return (T arg) =>
{
TResult result;
if (cache.TryGetValue(arg, out result))
{
return result;
}
else
{
result = function(arg);
cache.Add(arg, result);
return result;
}
};
}
When you pass a delegate to Memoize, it will return a new delegate that only ever calls your original one if it's called with an argument it has not seen before; otherwise it supplies the answer from its cache of previous results. Obviously you'll only want to use this on delegates whose results are wholly dependent on the input parameters: if you've got a function that uses the current time, for example, caching results will get you stale answers.
So we can do this:
Func<long, long> findSequenceLength = null;
findSequenceLength = (long n) =>
{
if (n == 1) { return 1; }
var nextTerm = n.IsEven() ? n / 2 : 3* n + 1;
return findSequenceLength(nextTerm) + 1;
};
findSequenceLength = findSequenceLength.Memoize();
Now, because the original lambda stored in findSequenceLength is defined to call whatever delegate is stored in the findSequenceLength variable, when we store the memoized version of the lambda back into findSequenceLength the result is a recursive function that can short-cut any calculations for parameters that it has seen before.
I'll let you untwist your brain before I carry on.
Recovered? Now the final answer is just a step away.
Using our findSequenceLength lambda we can calculate the sequence length for any number we like. But to get the final answer to the problem we don't actually want to know the sequence length: we need to know which number generates the longest sequence. So we can't just generate all the sequence lengths and find the maximum over that set. Instead, we'll generate objects containing both the starting number and the sequence length, and use my MaxItem extension method which finds the maximum object in a sequence, using which ever property of the object you grab with a lambda expression to make the comparison. Like so:
return 1.To(1000000)
.Select(n => new { n, Length = findSequenceLength(n) })
.MaxItem(info => info.Length)
.n;
The full code is shown below, together with the code for
MaxItem. Or you can download it from my
Project Euler page on MSDN Code Gallery.
Oh, and what difference in performance does Memoization make? 0.85 seconds to run the code on my machine compared with 4.4 seconds when I take out the call to Memoize().
[EulerProblem(14, Title = "Find the longest sequence using a starting number under one million.")]
public class Problem14
{
public long Solve()
{
Func<long, long> findSequenceLength = null;
findSequenceLength = (long n) =>
{
if (n == 1) { return 1; }
var nextTerm = n.IsEven() ? n / 2 : 3 * n + 1;
return findSequenceLength(nextTerm) + 1;
};
findSequenceLength = findSequenceLength.Memoize();
return 1.To(1000000)
.Select(n => new { n, Length = findSequenceLength(n) })
.MaxItem(info => info.Length)
.n;
}
}
public static T MaxItem<T, TCompare>(this IEnumerable<T> sequence, Func<T, TCompare> comparatorSelector) where TCompare : IComparable<TCompare>
{
T max = sequence.First();
TCompare maxComparator = comparatorSelector(max);
foreach (var item in sequence)
{
var comparator = comparatorSelector(item);
if (comparator.CompareTo(maxComparator) > 0)
{
max = item;
maxComparator = comparator;
}
}
return max;
}