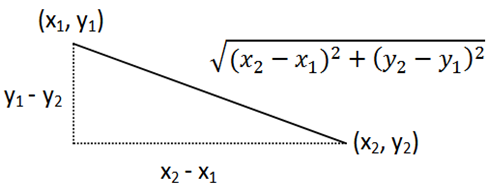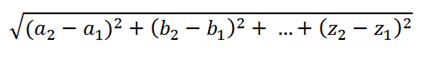WPF MVVM Commands - new reduced-boilerplate recipe

Morgan Skinner, an Application Development Consultant with Microsoft UK, had a post on his blog yesterday complaining at the quantity of boilerplate code needed to create commands in ViewModels for WPF and Silverlight. I share his irk about that.

He shows a clever technique involving ICustomTypeDescriptor that avoids creating properties (and hence backing fields) for each of the commands. But I think he goes too far. Without the properties on the ViewModel, its tests are going to have a hard time knowing what commands it exposes; and accessing them through code isn’t going to be as straightforward as a property access.

So I propose an alternative technique. It boils down to this:

public class MyViewModel : ViewModelBase
{
    public ICommand Demonstrate
    {
        get
        {
            return Commands.GetOrCreateCommand(
                () => this.Demonstrate,
                DoDemonstration,
                IsFeelingDemonstrative);
        }
    }

    private void DoDemonstration()
    {
        MessageBox.Show("Ta da!");
    }

    private bool IsFeelingDemonstrative()
    {
        return DateTime.Today.DayOfWeek == DayOfWeek.Friday;
    }
}

As you can see, ViewModelBase is providing a Commands property to manage all the commands. This neatly avoids having to create a field for each one. Commands is an instance of CommandHolder which is equally simple:

public class ViewModelBase : INotifyPropertyChanged
{
    CommandHolder _commandHolder = new CommandHolder();

    // snipped Property Change stuff

    protected CommandHolder Commands
    {
        get
        {
            return (_commandHolder ?? (_commandHolder = new CommandHolder()));
        }
    }
}

public class CommandHolder
{
    Dictionary<string, ICommand> _commands = new Dictionary<string, ICommand>();

    public ICommand GetOrCreateCommand<T>(
        Expression<Func<T>> commandNameExpression, 
        Action executeCommandAction, 
        Func<bool> canExecutePredicate)
    {
        return GetOrCreateCommand(
            commandNameExpression,
            parameter => executeCommandAction(),
            parameter => canExecutePredicate());    
    }

    public ICommand GetOrCreateCommand<T>(
        Expression<Func<T>> commandNameExpression, 
        Action<object> executeCommandAction, 
        Func<object, bool> canExecutePredicate)
    {
        var commandName = SymbolHelpers.GetPropertyName(commandNameExpression);

        if (!_commands.ContainsKey(commandName))
        {
            var command = new DelegateCommand(executeCommandAction, canExecutePredicate);
            _commands.Add(commandName, command);
        }

        return _commands[commandName];
    }
}

What do you think? Are my concerns about testa-reada-bility warranted? Does my technique eliminate enough of the boilerplate?

I’ve put a full sample on MSDN code gallery.

Project Euler 59: Cracking an XOR code

Code breaking is about as glamorous as it gets for a Geek. So when it comes to Project Euler Problem 59, think 24, with Jack Bauer unscathed amidst a hail of bullets, memory stick in one hand, terrorist’s neck throttled in the other, threatening terrible retribution to the bad guy’s family if the secret goes to the grave with him. Terrorist rasps out,

“There’s a file … cipher1.txt … ASCII format … urrrh … XOR … 3 … letter … password … lower case … all English”

What would Chloe O’Brian make of that when she received the file over a secure socket from Jack’s Smart Phone? Being the bright girl she is, I’ve no doubt that she’d fire up MonoDevelop (only the dumb FBI would use Visual Studio and Windoze) and write the following:

var encryptedBytes = File.ReadAllText(dataPath)
                        .Split(',')
                        .Select(byte.Parse)
                        .ToArray();

That would get her the encrypted data from the file as a sequence of bytes. Now to generate all possible passwords:

const byte FirstChar = (byte)'a';
const byte LastChar = (byte)'z';

var allPossiblePasswords = from a in FirstChar.To(LastChar)
                           from b in FirstChar.To(LastChar)
                           from c in FirstChar.To(LastChar)
                           select new[] { a, b, c };

XOR encryption requires that the password be repeated cyclically, abcabcabc.... So given a sequence containing the characters of password, how about a Repeat extension method that repeats the sequence ad infinitum? (if you look at the following code and hear the Infinite Loop alarms go off, remember that iterators are lazily evaluated):

public static IEnumerable<T> Repeat<T>(this IEnumerable<T> sequence)
{
    while (true)
    {
        foreach (var item in sequence)
        {
            yield return item;
        }
    }
}

While she’s at it, she’ll need to Xor two sequences together:

public static IEnumerable<byte> Xor(this IEnumerable<byte> sequenceA, IEnumerable<byte> sequenceB)
{
    return sequenceA.Zip(sequenceB, (left, right) => (byte)(left ^ right));
}

This uses the Zip method, new in .Net 4.0, which merges two sequences together, allowing elements from left and right sequences to be processed in pairs (if you’re surprised, as I was, that the (byte) cast is necessary, see this question on Stack Overflow).

Now she can try out all the passwords, seeing what they give her if she uses them to decrypt the text. Note that Chloe has already adopted .Net 4.0 and the PLINQ extensions, so she’s using AsParallel() to max out her 128 Core workstation. (ConvertAsciiBytesToString is another extension method that simply delegates to ASCIIEncoding.GetString).

var possibleDecryptions = from trialPassword in allPossiblePasswords.AsParallel()
                          let repeatedPassword = trialPassword.Repeat()
                          select encryptedBytes
                                          .Xor(repeatedPassword)
                                          .ConvertAsciiBytesToString();

But she’s hardly going to spend the next 24 hours trawling through the possible decryptions to pick out the one in recognisable English from the 17575 in gobledygook. So she needs some means of assessing them automatically. This is where Chloe is forever in my debt. She read last weeks episode of Functional Fun, so she knows about my LanguageAnalyser that uses frequency analysis to determine how likely a sample of text is to be written in a particular language.

Rather than using the analyser to determine which of several languages the sample is written in, Chloe can use her prior knowledge that the coded message is written in English, and determine which of the possible decryptions has letter frequencies that most closely match those in English.

var languageAnalyser = new LanguageAnalyser();

var decryptionsWithDistanceToEnglish = from decryptedString in possibleDecryptions
                                       select new
                                                  {
                                                      DecryptedString = decryptedString,
                                                      Distance = languageAnalyser.DetermineCloseness(decryptedString, LanguageProfiles.English)
                                                  };

var mostLikelyDecryption = decryptionsWithDistanceToEnglish.MinItem(p => p.Distance);

And that's it. Thanks to Linguistic Geometry and LINQ, Chloe can report the decrypted (and surprisingly biblical!) message to Jack, so that he can get on with saving the world.

Ahem. Before we got carried away we were trying to solve Project Euler Problem 59, and that asks for the sum of the Ascii values of the decrypted message. So we need one more step:

var sumOfAsciiValues = mostLikelyDecryption.DecryptedString
                        .ConvertStringToAsciiBytes()
                        .Aggregate(0, (runningTotal, next) => runningTotal += next);

The full code is shown below, and is also available on MSDN Code Gallery.

namespace ProjectEuler
{
    [EulerProblem(59, Title="Using a brute force attack, can you decrypt the cipher using XOR encryption?")]
    public class Problem59
    {
        public long Solve()
        {
            const byte FirstChar = 97;
            const byte LastChar = 122;

            var dataPath = @"ProblemData\Problem59.txt";

            var encryptedBytes = File.ReadAllText(dataPath)
                                    .Split(',')
                                    .Select(byte.Parse)
                                    .ToArray();

            var allPossiblePasswords = from a in FirstChar.To(LastChar)
                                       from b in FirstChar.To(LastChar)
                                       from c in FirstChar.To(LastChar)
                                       select new[] { a, b, c };

            var possibleDecryptions = from trialPassword in allPossiblePasswords.AsParallel()
                                      let repeatedPassword = trialPassword.Repeat()
                                      select encryptedBytes
                                          .Xor(repeatedPassword)
                                          .ConvertAsciiBytesToString();

            var languageAnalyser = new LanguageAnalyser();

            var decryptionsWithDistanceToEnglish = from decryptedString in possibleDecryptions
                                                   select new
                                                              {
                                                                  DecryptedString = decryptedString,
                                                                  Distance = languageAnalyser.DetermineCloseness(decryptedString, LanguageProfiles.English)
                                                              };

            var mostLikelyDecryption = decryptionsWithDistanceToEnglish.MinItem(p => p.Distance);

            var sumOfAsciiValues = mostLikelyDecryption.DecryptedString
                .ConvertStringToAsciiBytes()
                .Aggregate(0, (runningTotal, next) => runningTotal += next);

            return sumOfAsciiValues;
        }
    }
}

Practical Linq #5: Guessing the language of a piece of text

Google Chrome is magic: getting ready for my summer holiday to Brugge, I hit the city’s homepage. A little bar popped up at the top of the page: “This page is in Dutch. Would you like to translate it?”

How does Chrome know that? I suppose the domain name “.be” is one clue, but they speak French as well as Dutch in Belgium, so that by itself is not enough. Chrome does the same trick for pages written in a whole raft of languages, from Afrikaans to Yiddish.

I don’t know what Google’s secret sauce is, but I can show you one simple and surprisingly effective technique with an elegant implementation using LINQ in C#.

Studies in Linguistic Geometry

It is built around the observation that in each sufficiently large sample of text in a given language, letters of the alphabet will all occur with roughly the same frequencies. In English for example, the letter ‘e’ tops the popularity charts, making up about 13% of the average body of text. ‘t’ and ‘a’ are next, accounting for 9% and 8%. By contrast, in Portuguese, ‘a’ is the most frequent, at 15%, with ‘e’ and ‘o’ close behind.

So letter frequencies can be used as a kind of signature, or DNA profile, for a language. But given a sample of text, how do we decide which language signature it matches most closely? This is where we switch from linguistics to geometry.

In 2-dimensional space, we calculate the distance between two points using Pythagoras’ theorem. 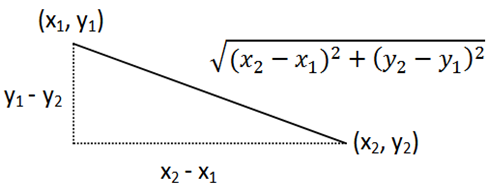The same thing works for two points in the real, 3-d, world. The distance from (x1, y1, z1) to (x2, y2, z2) is

But why stop there? What about the distance between two points in 26-dimensional space? You guessed it!

26-d space? Why bring that into the equation? Well think about those language signatures, giving the frequency of occurrence of each letter. You can reinterpret those signatures as points in 26-d space: the point representing the signature for English would be at 0.13 along the ‘e’ axis, 0.09 along the ‘t’ axis, 0.08 along the ‘a’ axis, and so on.

This then gives us our straightforward method of determining which language our sample text belongs to. We do a frequency analysis on its letters, then imagine the result of that analysis as a point in 26-d space, and work out which language signature it lies closest to using Pythagoras. Easy!

So how does it look in LINQ?

Linq to Linguistics

We start off with the frequency analysis (taking care to normalise the text to lower-case):

IEnumerable<CharacterFrequency> CalculateCharacterFrequencies(string sample)
{
    var characterFrequencies = sample
        .Select(char.ToLower)
        .GroupBy(c => c)
        .Select(group => new CharacterFrequency
        {
            Character = group.Key,
            Frequency = (double)group.Count() / sample.Length
        });

    return characterFrequencies;
}

Next we introduce a LanguageSignature class to hold the signature of each language:

[DebuggerDisplay("Language = { Language }")]
public class LanguageSignature
{
    private IDictionary<char, double> _frequencies;

    public LanguageSignature(string language, IDictionary<char, double> characterFrequencies)
    {
        Language = language;
        _frequencies = characterFrequencies;
    }

    public string Language { get; protected set; }

    public double GetFrequency(char character)
    {
        double frequency;
        return _frequencies.TryGetValue(character, out frequency) ? frequency : 0;
    }
}

Here are some snippets of sample signatures, data courtesy of Wikipedia

public static class LanguageSignatures
{
    public static LanguageSignature English =
        new LanguageSignature(
            "English",
            new Dictionary<char, double>
                {
                    {'a', 0.08167},
                    {'b', 0.01492},
                    {'c', 0.02782},
                    /// etc.
                });

    public static LanguageSignature French =
        new LanguageSignature(
            "French",
            new Dictionary<char, double>
                {
                    {'a', 0.07636},
                    {'b', 0.00901},
                    // etc.
                });

    
}

Now we do our sums in 26-d space, ignoring any letters that we don’t have frequency data for (note that Sqrt is a little extension method I created on the Double class that simply calls Math.Sqrt):

double CalculateDistanceFromSignature(LanguageSignature signature, IEnumerable<CharacterFrequency> characterFrequencies)
{
    var distance = characterFrequencies
        .Where(characterFrequency => signature.GetFrequency(characterFrequency.Character) > 0)
        .Select(characterFrequency
            => Math.Pow(characterFrequency.Frequency - signature.GetFrequency(characterFrequency.Character), 2))
        .Sum()
        .Sqrt();
    return distance;
}

Now we’re ready to determine which language our sample is closest to:

public LanguageSignature DetermineMostLikelyLanguage(string sample, IEnumerable<LanguageSignature> signatures)
{
    var characterFrequencies = CalculateCharacterFrequencies(sample);

    var closestLanguage = signatures.Select(signature => new
    {
        Language = signature,
        Distance = CalculateDistanceFromSignature(signature, characterFrequencies)
    })
    .MinItem(languageDistance => languageDistance.Distance);

    return closestLanguage.Language;
}

MinItem is an extension method I knocked up that returns the item from a sequence that yields the smallest value from the expression you supply (in this case, the smallest distance):

public static T MinItem<T, TCompare>(this IEnumerable<T> sequence, Func<T, TCompare> comparatorSelector) where TCompare : IComparable<TCompare>
{
    var minItem = sequence.Aggregate(
        sequence.First(), 
        (current, min) => comparatorSelector(current).CompareTo(comparatorSelector(min)) < 0 ? current : min);

    return minItem;
}

And we’re done.

Testing, Testing, Un, deux, trois

To prove it, I created a little test that analysed samples of texts in several languages taken from Project Gutenberg (the test uses MbUnit’s very handy XmlData feature to read the different test cases from my xml file).

public class LanguageAnalyserTests
{
    [Test]
    [XmlData("//Sample", FilePath = "ProblemData\\LanguageSamples.xml")]
    public void TestAnalysis([Bind("Text")]string text, [Bind("@Language")]string expectedLanguage)
    {
        var analyser = new LanguageAnalyser();
        var determinedLanguage = analyser.DetermineMostLikelyLanguage(
            text
            new[] { LanguageSignatures.English, LanguageSignatures.French, LanguageSignatures.German, LanguageSignatures.Dutch, LanguageSignatures.Spanish, LanguageSignatures.Italian });

        Assert.AreEqual(expectedLanguage, determinedLanguage.Language);
    }
}

In my test I’ve got 9 samples in German, English, French, Dutch, Spanish and Italian, extracted at random from the Gutenberg archives and each sample is correctly identified by my analyser. I also did a little experiment to see how much text it needed to correctly distinguish the samples. Limiting the samples to 600 characters caused some confusion between Spanish and English, but 700 characters was sufficient in my tests to enable the analyser to pick the right language for all samples.

A Challenge

I actually developed this LanguageAnalyser to help me solve a problem on Project Euler. Which one was it? Answers in the comments please, or by email, and bonus marks to anybody who can guess what my solution looks like. Check back Monday for the answer, and for full source code to today’s post.

Update: The answer's here, and the source code is now on MSDN Code Gallery